ベクトルを用いた三角形の面積公式3種類
本記事では, ベクトルの分野で基本的な3つの面積公式とその導出方法を紹介します。
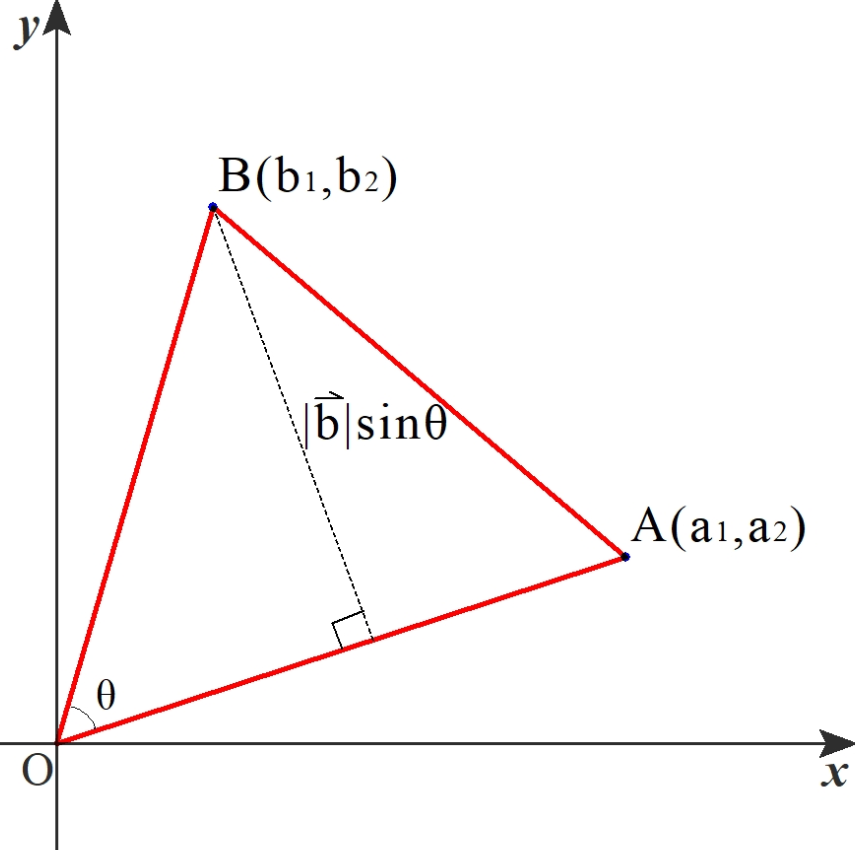
\(\overrightarrow{OA}=\overrightarrow{a}\,(a_1,a_2)\)
\(\overrightarrow{OB}=\overrightarrow{b}\,(b_1,b_2)\) とすると
三角形OABの面積 \(S\) は
\((1)\,\color{blue}{S=\dfrac{1}{2}|\vec{a}||\vec{b}|\sin{\theta}}\)
\((2)\,\color{blue}{S=\dfrac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}}\)
\((3)\,\color{blue}{S=\dfrac{1}{2}|a_1b_2-a_2b_1|}\)
(1)について
\(|\vec{b}|\sin{\theta}\)はOAを底辺としたときの高さであるため、『三角形の面積=底辺×高さ÷2』の公式をそのまま使っています。
底辺 \(OA=|\vec{a}|\)
高さ \(|\vec{b}|\sin{\theta}\)
の三角形の面積は \(\dfrac{1}{2}|\vec{a}||\vec{b}|\sin{\theta}\)
(1)から(2)の導出
\dfrac{1}{2}|\vec{a}||\vec{b}|\sqrt{1-\cos^2{\theta}}\)
\(=\dfrac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2(1-\cos^2{\theta}})\)
\(=\dfrac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-
|\vec{a}|^2|\vec{b}|^2\cos^2{\theta}}\)
\(=\dfrac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}\)
最後は内積の定義 \(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos \theta\)を使って変形しました。
逆をたどれば\((2)\rightarrow(1)\)も示せます。
(2)から(3)の導出
\(|\vec{a}|^2=a_1^2+a_2^2\)
\(|\vec{b}|^2=b_1^2+b_2^2\)
\(\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2\)
したがって,
\(S\)
\(=\displaystyle\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}\)
\(\displaystyle =\frac{1}{2}\sqrt{(a_1^2+a_2^2)(b_1^2+b_2^2)-(a_1b_1+a_2b_2)^2}\)
\(\displaystyle=\frac{1}{2}\sqrt{a_1^2b_2^2-2a_1b_1a_2b_2+a_2^2b_1^2}\)
\(=\dfrac{1}{2}\sqrt{(a_1b_2-a_2b_1)^2}=\dfrac{1}{2}|a_1b_2-a_2b_1|\)
逆をたどれば\((3)\rightarrow(2)\)も示せます。
問題を解くときは, 何が与えられるかで公式を使い分けましょう。
例)
・ベクトルの大きさと角度が分かるときは(1)を使いやすい
・角度が不明で, ベクトルの内積と大きさが分かるときは(2)を使いやすい
・ベクトルの成分が分かるとき(各点の座標が分かるとき)は(3)を使いやすい
