関数f(x)がx=aで微分可能ならばx=aで連続であることの証明
関数 \(f(x)\) が \(x=a\) で微分可能ならば \(f(x)\) は \(x=a\) で連続であることの証明と,逆が成り立たないことについて説明します。
証明
【方針】
\(\phantom{[1]\quad}\Leftrightarrow\displaystyle\lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}\) が存在する (この極限値を\(f'(a)\)で表す)
\(\)
[2] \(f(x)\) が \(x=a\) で連続
\(\phantom{[2]\quad}\Leftrightarrow\displaystyle\lim_{x\to a}f(x)=f(a)\) が成り立つ
【証明】
関数 \(f(x)\) が \(x=a\) で微分可能だから
\(\displaystyle\lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}\) が存在する。
よって,
\(\phantom{=}\displaystyle\lim_{x\to a}\{f(x)-f(a)\}\\
=\displaystyle\lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}\cdot (x-a)\\
=f'(a)\cdot0 \\
=0\)
\(\therefore\quad \displaystyle\lim_{x\to a}f(x)=f(a)\)
したがって, \(f(x)\) は \(x=a\) で連続である。(証明終)
極限には次の性質があります。
上の【証明】ではこの性質から
\(\displaystyle\lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}=f'(a),\, \lim_{x\to a}(x-a)=0 \,\,\Rightarrow\,\, \lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}\cdot(x-a)=f'(a)\cdot 0\)
であることを利用しています。
この性質を使う問題は極限が存在するように定数を定める問題で扱っています。
上で示したように,定理
「関数 \(f(x)\) が \(x=a\) で微分可能ならば, \(f(x)\) は \(x=a\) で連続である。」
が成り立つので,その対偶
「関数 \(f(x)\) が \(x=a\) で連続でないならば, \(f(x)\) は \(x=a\) で微分可能でない。」
も成り立ちます。
逆は成り立たない
この定理の逆
「関数 \(f(x)\) が \(x=a\) で連続ならば, \(f(x)\) は \(x=a\) で微分可能である。」
は成り立たないです。
例えば, 関数 \(f(x)=|x|\) は \(x=0\) で連続ですが, \(x=0\) で微分可能ではありません。
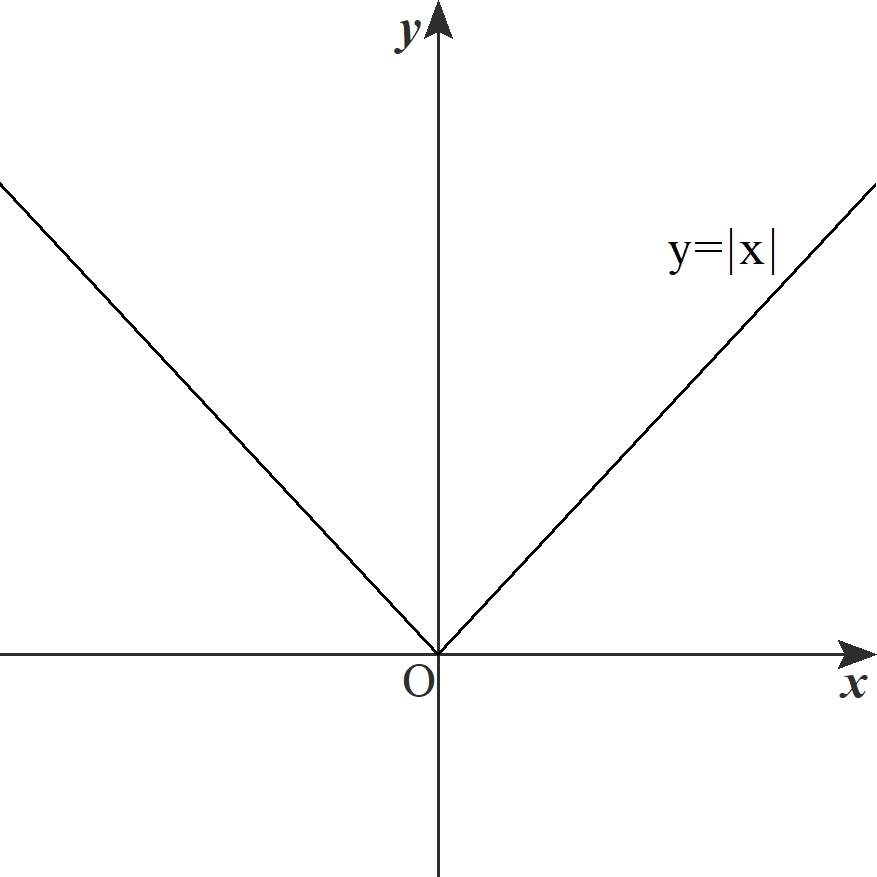
\(\displaystyle \lim_{x\to 0}f(x)=\lim_{x\to 0}|x|=0\)
\(f(0)=0\)
であるから,
\(\displaystyle \lim_{x\to 0}f(x)=f(0)\)
よって, \(f(x)\) は \(x=0\) で連続である。
一方,
\(\displaystyle \lim_{h\to +0}\dfrac{f(0+h)-f(0)}{h}=\lim_{h\to +0}\dfrac{|h|}{h}=\lim_{h\to +0}\dfrac{h}{h}=1\)
\(\displaystyle \lim_{h\to -0}\dfrac{f(0+h)-f(0)}{h}=\lim_{h\to -0}\dfrac{|h|}{h}=\lim_{h\to -0}\dfrac{-h}{h}=-1\)
よって, 右側極限と左側極限が一致しないので,
\(\displaystyle \lim_{h\to 0}\dfrac{f(0+h)-f(0)}{h}\) は存在しない。
したがって, \(f(x)\) は \(x=0\) で微分可能ではない。(証明終)
