【積分】1/6公式と1/12公式の証明

上記の公式が成り立つことを実際に計算して確認します。
展開してごり押しで計算することも可能ですが, 手間がかかります。
\((x-\alpha)\) または \((x-\beta)\) のカタマリを作って
\(\displaystyle\int (x-\alpha)^{n}\,dx=\dfrac{1}{n+1}(x-\alpha)^{n+1}\)
を利用することで計算が楽になります。

---

(1) の証明
\(\phantom{=}\displaystyle \int_{\alpha}^{\beta}(x-\alpha)(x-\beta)\,dx\)
\(=\displaystyle \int_{\alpha}^{\beta}(x-\alpha)(x\color{red}{-\alpha+\alpha}-\beta)\,dx\)
\(=\displaystyle \int_{\alpha}^{\beta}(x-\alpha)\{(x-\alpha)-(\beta -\alpha)\}\,dx\)
\(=\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^2-(\beta -\alpha)(x-\alpha)\,dx\)
\(=\left[\dfrac{1}{3}(x-\alpha)^3 – \dfrac{1}{2}(\beta \, – \alpha)(x-\alpha )^2 \right]_{\alpha}^{\beta}\)
\(=\dfrac{1}{3}(\beta\, -\alpha)^3 – \dfrac{1}{2}(\beta \, -\alpha)^3\)
\(=-\dfrac{1}{6}(\beta \,- \alpha)^3\)

---

(2) の証明
\(\phantom{=}\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^2(x-\beta)\,dx\)
\(=\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^2(x\color{red}{-\alpha +\alpha} -\beta)\,dx\)
\(=\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^2\{(x-\alpha)\,-(\beta \,- \alpha)\}\,dx\)
\(=\displaystyle \int_{\alpha}^{\beta}\{(x-\alpha)^3\, – (\beta \,- \alpha)(x-\alpha)^2\}\,dx\)
\(=\left[ \dfrac{1}{4}(x \,- \alpha)^4 -\dfrac{1}{3}(\beta \, -\alpha)(x-\alpha)^3 \right]_{\alpha}^{\beta}\)
\(=\dfrac{1}{4}(\beta \, -\alpha)^4 – \dfrac{1}{3}(\beta \, -\alpha)^4\)
\(=-\dfrac{1}{12}(\beta \, -\alpha)^4\)

---

(3) の証明
\(\phantom{=}\displaystyle \int_{\alpha}^{\beta}(x-\alpha)(x-\beta)^2\,dx\)
\(=\displaystyle \int_{\alpha}^{\beta} (x\color{red}{-\beta + \beta}-\alpha)(x-\beta)^2\)
\(=\displaystyle \int_{\alpha}^{\beta}\{ (x\,- \beta) -(\alpha\,- \beta)\}(x-\beta)^2\,dx\)
\(=\displaystyle \int_{\alpha}^{\beta}\{ (x\,- \beta)^3 -(\alpha\,- \beta)(x \,-\beta)^2\}\,dx\)
\(=\left[\dfrac{1}{4}(x \,-\beta)^4- \dfrac{1}{3}(\alpha \,-\beta)(x\,-\beta)^3\right]_{\alpha}^{\beta}\)
\(=-\dfrac{1}{4}(\alpha \,-\beta)^4 + \dfrac{1}{3}(\alpha \,-\beta)^4\)
\(=\dfrac{1}{12}(\alpha\,-\beta)^4 \\
=\dfrac{1}{12}(\beta\,-\alpha)^4\)

上図のように, 放物線 \(C:\,y=ax^2+bx+c\,\,(a>0)\) と直線 \(l:\,y=mx+n\) が2点で交わり, 交点の \(x\) 座標が \(\alpha,\,\beta\) であるとき, \(C\) と \(l\) で囲まれた部分の面積を \(S\) とすれば,
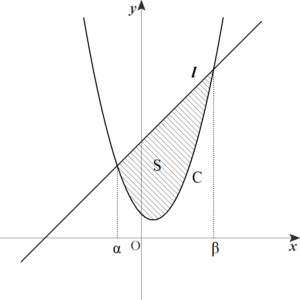
\(\displaystyle S=\int_{\alpha}^{\beta}\{(mx+n)-(ax^2+bx+c)\}\,dx\)
\(\displaystyle \phantom{S}=\int_{\alpha}^{\beta} -a(x-\alpha)(x-\beta)\,dx\)
\(\displaystyle \phantom{S}=(-a)\cdot (-\dfrac{1}{6}) \cdot (\beta-\alpha)^3\)　(∵公式(1))
\(\displaystyle \phantom{S}=\color{red}{\dfrac{a}{6}(\beta-\alpha)^3}\)

上図のように, 曲線 \(C:\,y=ax^3+bx^2+cx+d\,\,(a>0)\) と直線 \(l:\,y=mx+n\) が \(x=\alpha\) で接し, \(x=\beta\) で交わるとき, \(C\) と \(l\) で囲まれた部分の面積を \(S\) とすれば,
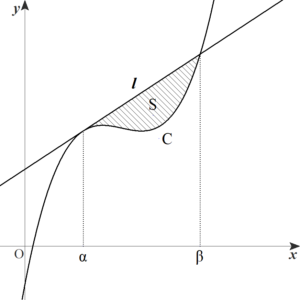
\(\displaystyle S=\int_{\alpha}^{\beta}\{(mx+n)-(ax^3+bx^2+cx+d)\}\,dx\)
\(\displaystyle \phantom{S}=\int_{\alpha}^{\beta} -a(x-\alpha)^2(x-\beta)\,dx\)
\(\displaystyle \phantom{S}=(-a)\cdot (-\dfrac{1}{12}) \cdot (\beta-\alpha)^4\) 　(∵公式(2))
\(\displaystyle \phantom{S}=\color{red}{\dfrac{a}{12}(\beta-\alpha)^4}\)

上図のように, 曲線 \(C:\,y=ax^3+bx^2+cx+d\,\,(a>0)\) と直線 \(l:\,y=mx+n\) が \(x=\alpha\) で交わり, \(x=\beta\) で接するとき, \(C\) と \(l\) で囲まれた部分の面積を \(S\) とすれば,
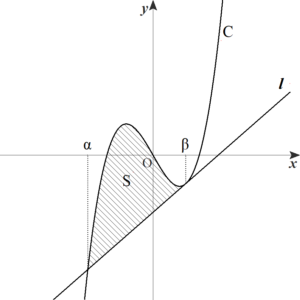
\(\displaystyle S=\int_{\alpha}^{\beta}\{(ax^3+bx^2+cx+d)-(mx+n)\}\,dx\)
\(\displaystyle \phantom{S}=\int_{\alpha}^{\beta} a(x-\alpha)(x-\beta)^2\,dx\)
\(\displaystyle \phantom{S}=a \cdot \dfrac{1}{12}(\beta-\alpha)^4\)　(∵公式(3))
\(\displaystyle \phantom{S}=\color{red}{\dfrac{a}{12}(\beta-\alpha)^4}\)