3次関数の極大値・極小値を次数を下げて求める問題
『\(x^3-3x^2+x+1\) の極大値を求めよ』
といったような, 3次関数の極値を求める問題の解法を紹介します。
解が複雑なときは次数を下げる
関数 \(f(x)\) の極値を調べるとき, \(f^{\prime}(x)=0\) を解きます。
\(f'(x)=0\) の解が \(x=\alpha\) であれば, \(f(\alpha)\) が極値です。
\(\alpha\) が簡単な形であれば \(f(\alpha)\) も簡単に求まります。
しかし,
\(\alpha=\dfrac{\bigcirc +\sqrt{\bigcirc}}{\bigcirc}\)
のように, \(\alpha\) が分数もルートも含んだ複雑な形の場合, \(f(\alpha)\) をそのまま計算するのは得策ではありません。
このような場合, \(f(x)\) を \(f^{\prime}(x)\) で割った式を使うと計算が楽になります。
\(f(x)\) を \(f^{\prime}(x)\) で割って次数下げ
3次関数 \(f(x)\) を \(f^{\prime}(x)\) で割ったときの商を\(Q(x)\) , 余りを\(Ax+B\) とおくと,
\(f(x)=f^{\prime}(x)\, Q(x)+Ax+B\)
となります。(\(f^{\prime}(x)\) は2次式で, 整式を2次式で割った余りは1次式 \(Ax+B\) で表せます。)
\(x=\alpha\) が極値だとすると, \(f^{\prime}(\alpha)=0\) なので, 上式に \(x=\alpha\) を代入すると
\(f(\alpha)\)
\(=f^{\prime}(\alpha)\, Q(\alpha)+A\alpha+B\)
\(=A\alpha +B\)
になります。
つまり, 極値\(f(\alpha)\) を求めたければ, \(A\alpha +B\) を計算すればよいです。
例題と解答
問題
解答
\(f^{\prime}(x)=3x^2-6x+1\)
\(f^{\prime}(x)=0\) を解くと,
\(x=\dfrac{3\pm \sqrt{6}}{3}\)
\(x^3\) の係数は正だから,\(f(x)\) のグラフは下図のようになる。
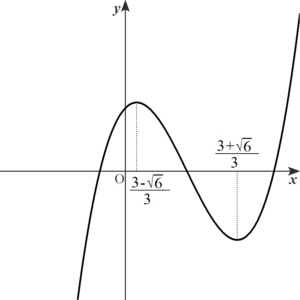
よって \(\alpha=\dfrac{3-\sqrt{6}}{3}\) とおくと, 極大値は \(f(\alpha)\)
\(f(x)\) を\(f^{\prime}(x)\) で割ると,
\require{enclose}
\begin{array}{r}
\dfrac{1}{3}x -\dfrac{1}{3}\phantom{000000000}\\
3x^2-6x+1\enclose{longdiv}{\phantom{0}x^3-3x^2+\phantom{0}x+1} \\
\underline{{x^3-2x^2+\dfrac{1}{3}x\phantom{000}}} \\
-x^2+\dfrac{2}{3}x+1 \\
\underline{-x^2+2x-\dfrac{1}{3}} \\
-\dfrac{4}{3}x+\dfrac{4}{3} \\
\end{array}
\)
したがって,
\(f(x)=f^{\prime}(x)\left(\dfrac{1}{3}x-\dfrac{1}{3}\right)-\dfrac{4}{3}x+\dfrac{4}{3}\)
\(x=\alpha\) を代入すると,
\(f(\alpha)=\color{blue}{\underbrace{f^{\prime}(\alpha)}_{=0}}\left(\dfrac{1}{3}\alpha-\dfrac{1}{3}\right)-\dfrac{4}{3}\alpha+\dfrac{4}{3}\)
\(=-\dfrac{4}{3}\alpha +\dfrac{4}{3}\)
\(=-\dfrac{4}{3}(\alpha -1)\)
\(=-\dfrac{4}{3}\cdot \left(-\dfrac{\sqrt{6}}{3}\right)\)
\(=\color{red}{\dfrac{4\sqrt{6}}{9}}\)
