サイクロイドの微分・面積・体積・弧長
サイクロイドでよく問われる事項の計算方法を紹介します。
数Ⅲの知識をフルに使います。
サイクロイドの媒介変数表示
\(a\)を正の定数, \(t\) を媒介変数として
\(\left\{ \begin{array}{l}
x=a(t-\sin t )\\
y=a(1-\cos t)\\
\end{array} \right.\)
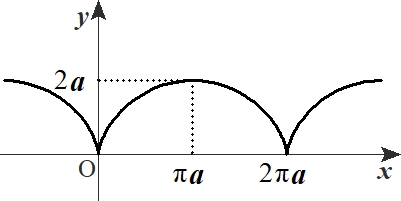
で表される曲線をサイクロイドとよび、下の図のようなグラフになります。
導関数・第2次導関数
\(\dfrac{dy}{dx},\quad\dfrac{d^2y}{dx^2}\)
を\(t\) で表します。
\(\dfrac{dx}{dt}=a(1-\cos t)\)
よって
\(\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\color{red}{\dfrac{\sin t}{1-\cos t}}\)
\(\dfrac{d^2y}{dx^2}\)
\(=\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\)
\(=\dfrac{dt}{dx}\dfrac{d}{dt}\left(\dfrac{dy}{dx}\right)\)
\(=\dfrac{1}{\dfrac{dx}{dt}}\dfrac{d}{dt}\left(\dfrac{\sin t}{1-\cos t}\right)\)
\(=\dfrac{1}{a(1-\cos t)}\dfrac{\cos t(1-\cos t) -\sin^2 t}{(1-\cos t)^2}\)
\(=\dfrac{\cos t -1}{a(1-\cos t)^3}\)
\(=\color{red}{-\dfrac{1}{a(1-\cos t)^2}}\)
x軸で囲まれた面積
\(\left\{ \begin{array}{l}
x=a(t-\sin t )\\
y=a(1-\cos t)\\
\end{array} \right. (0\leqq t \leqq 2\pi)\)
とx軸に囲まれた部分の面積\(S\)を求めます。
\(\begin{array}{l|l}
x & 0\rightarrow 2\pi a \\
\hline
t & 0\rightarrow 2\pi \\
\end{array}
\)
\(y=a(1-\cos t)\)
\(dx=\dfrac{dx}{dt}dt=a(1-\cos t)dt\)
より,
\(S\)
\(\displaystyle =\int_{0}^{2\pi}a^2 (1-\cos t)^2 dt\)
\(\displaystyle =a^2 \int_{0}^{2\pi}(1-2\cos t + \cos^2 t)dt\)
\(\displaystyle =a^2 \int_{0}^{2\pi}(1-2\cos t + \dfrac{1+\cos 2t}{2})dt\)
\(=a^2\left[\dfrac{3t}{2}-2\sin t+\dfrac{1}{4} \sin 2t\right]_{0}^{2\pi}\)
\(=a^2\cdot\dfrac{3}{2}\cdot 2\pi=\color{red}{3\pi a^2}\)
tだけの式に置換して, tで積分するのがポイントです。
x軸のまわりに1回転してできる立体の体積
\(\left\{ \begin{array}{l}
x=a(t-\sin t )\\
y=a(1-\cos t)\\
\end{array} \right. (0\leqq t \leqq 2\pi)\)
と \(x\) 軸に囲まれた図形を \(x\) 軸のまわりに1回転してできる立体の体積\(V\)を求めます。
\(\begin{array}{l|l}
x & 0\rightarrow 2\pi a \\
\hline
t & 0\rightarrow 2\pi \\
\end{array}
\)
\(y=a(1-\cos t)\)
\(dx=\dfrac{dx}{dt}dt=a(1-\cos t)dt\)
より,
\(V\)
\(\displaystyle =\pi\int_{0}^{2\pi}a^3 (1-\cos t)^3 dt\)
\(\displaystyle =\pi\int_{0}^{2\pi}a^3(1-3\cos t +3\cos^2 t -\cos^3 t )dt\)
\(\displaystyle =\pi a^3\int_{0}^{2\pi}\left(1-3\cos t + 3\cdot\dfrac{1+\cos 2t}{2} -\dfrac{\cos 3t + 3\cos t}{4}\right) dt\)
\(=\pi a^3 \left[\color{blue}{t}-3\sin t +\color{blue}{\dfrac{3t}{2}}+\dfrac{3\sin 2t}{4}-\dfrac{\sin 3t}{12} -\dfrac{3\sin t}{4}\right]_{0}^{2\pi}\)
\(=\pi a^3\color{blue}{\dfrac{5}{2}}\cdot 2\pi=\color{red}{5{\pi}^2 a^3}\)
補足
半角の公式、3倍角の公式を利用してcosの2乗や3乗を1乗の形にします。
\(\sin (n\pi)=0\)より、sinの項は全てゼロになります。
曲線の長さ
\(\left\{ \begin{array}{l}
x=a(t-\sin t )\\
y=a(1-\cos t)\\
\end{array} \right. (0\leqq t \leqq 2\pi)\)
で表されるサイクロイドの曲線の長さ\(L\)を求めます。
\(=\displaystyle \int_{0}^{2\pi}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,\,dt\)
\(=\displaystyle \int_{0}^{2\pi}\sqrt{a^2(1-\cos t)^2+ a^2\sin^2 t}\,\,dt\)
\(=\displaystyle a \int_{0}^{2\pi}\sqrt{1-2\cos t +\cos^2 t +\sin^2 t}\,\,dt\)
\(=\displaystyle a \int_{0}^{2\pi}\sqrt{2(1-\cos t)}\,\,dt\)
\(=\displaystyle a \int_{0}^{2\pi}\sqrt{2\cdot 2\sin^2 \dfrac{t}{2}}\,\,dt\)
\(=\displaystyle 2a \int_{0}^{2\pi}\sin \dfrac{t}{2}\,\,dt\)
\(=2a\left[-2\cos\dfrac{t}{2}\right]_0^{2\pi}\)
\(=2a\cdot(-2)\cdot(-1-1)=\color{red}{8a}\)
補足
曲線の長さの公式を使います。半角の公式を使ってsinの2乗を作ることでルートを外します。
\(0\leqq t/2 \leqq \pi\) のとき\(\sin (t/2)\) は正なのでルートを外すときに負になる心配はないです。
