偶関数・奇関数のいろいろな性質まとめ
偶関数・奇関数のいろいろな性質についてまとめています。
定義
\(f(-x)=f(x)\)
となるとき \(f(x)\) を偶関数という。
関数 \(f(x)\) が定義域内の任意の \(x\) について
\(f(-x)=-f(x)\)
となるとき \(f(x)\) を奇関数という。
グラフ
偶関数のグラフはy軸に関して対称です。
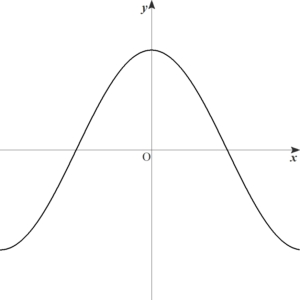
奇関数のグラフは原点に関して対称です。
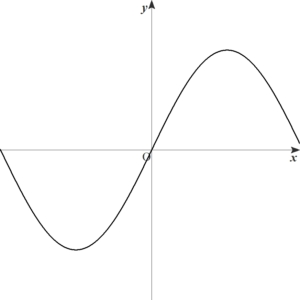
偶関数・奇関数の例,見分け方
・\(x^{\small\textbf{偶数}}\,\,(x^2,\,x^4,\,x^0=1,\,x^{-2}=\dfrac{1}{x^2}\,\small\text{など})\)
・\(\cos x\)
・定数関数
奇関数の例
・\(x^{\small\textbf{奇数}}\,\,(x,\,x^3,\,x^{-1}=\dfrac{1}{x}\,\small\text{など})\)
・\(\sin x\)
・\(\tan x\)
どちらでもない例
・\(2^x\)
・\(x^2+x\) (偶関数と奇関数の和)
見分け方
\(f(-x)\) を計算して
\(\phantom{-}f(x)\) と一致するなら偶関数
\(-f(x)\) と一致するなら奇関数
どちらとも一致しないなら偶関数でも奇関数でもない
\(\)
次の関数は偶関数か,奇関数か,どちらでもないか
(1) \(f(x)=x^4-3x^2+5\)
(2) \(g(x)=x^5+2x^3-4x\)
(3) \(h(x)=x^2+x+1\)
偶関数・奇関数の和差積商
\small\textbf{(奇関数) ± (奇関数) = (奇関数)}\\
\small\textbf{(偶関数) ± (奇関数) = (どちらでもない)}\)
\(\small\textbf{(偶関数) × (偶関数) = (偶関数)}\\
\small\textbf{(奇関数) × (奇関数) = (偶関数)}\\
\small\textbf{(偶関数) × (奇関数) = (奇関数)}\)
\(\small\dfrac{\textbf{(偶関数)}}{\textbf{(偶関数)}} = \textbf{(偶関数)}\)
\(\)
\(\small\dfrac{\textbf{(奇関数)}}{\textbf{(奇関数)}}=\textbf{(偶関数)}\)
\(\)
\(\small\dfrac{\textbf{(偶関数)}}{\textbf{(奇関数)}}=\textbf{(奇関数)}\)
\(\)
\(\small\dfrac{\textbf{(奇関数)}}{\textbf{(偶関数)}}=\textbf{(奇関数)}\)
偶関数の代表として \(x^2\),奇関数の代表として \(x\) を使えば確認しやすいです。
偶関数・奇関数の定積分
\(\displaystyle \int_{-a}^{a}\) のように,上端と下端で符号が異なるだけの定積分では,次の公式が成り立ちます。
\(f(x)\) が偶関数のとき
\(\displaystyle \int_{-a}^{a} f(x)\,dx=2\int_{0}^{a}f(x)\,dx\)
\(\)
\(f(x)\) が奇関数のとき
\(\displaystyle \int_{-a}^{a}f(x)\,dx=0\)
次の定積分を求めよ。
\((1)\quad \displaystyle\int_{-2}^{2}(3x^3+2x^2+x+1)\,dx\\
(2)\quad \displaystyle\int_{-\pi}^{\pi}x\cos x\,dx\)
偶関数・奇関数の微分
\(f(x)\) が偶関数のとき,\(f'(x)\) は奇関数
\(f(x)\) が奇関数のとき,\(f'(x)\) は偶関数
関数を偶関数と奇関数の和に分解する方法
\(f(x)=\underbrace{\dfrac{f(x)+f(-x)}{2}}_{g(x)}+\underbrace{\dfrac{f(x)-f(-x)}{2}}_{h(x)}\)
と分解できます。ここで,
\(g(-x)=\dfrac{f(-x)+f(x)}{2}=g(x)\)
より \(g(x)\) は偶関数であり,
\(h(-x)=\dfrac{f(-x)-f(x)}{2}=-h(x)\)
より \(h(x)\) は奇関数なので,\(f(x)\) は偶関数と奇関数の和になっています。
例えば, \(2^x\) は偶関数でも奇関数でもないですが,
\(2^x=\dfrac{2^x+\,2^{-x}}{2\quad}+\dfrac{2^x-\,2^{-x}}{2\quad}\)
というように,偶関数と奇関数の和で表せます。
