分数関数の極値を求める方法
分数関数の極値を求める方法について解説します。
特に, 極値を与える \(x\) が複雑なときに役立つテクニックを紹介します。
分数関数の極値を楽に求めるテクニック
分数関数の極値を与える \(x\) が複雑になるとき, 次の定理を使うと計算が楽になります。
定理と証明
\(f(x)=\dfrac{g(x)}{h(x)}\) について, \(f'(\alpha)=0,\,h'(\alpha)\neq 0\) ならば,
\(f(\alpha)=\dfrac{g'(\alpha)}{h'(\alpha)}\) が成り立つ。
この定理は, 数学講師の安田亨氏が発見したことから,「安田の定理」と呼ばれることもあります。以下, この呼び方を使います。
\(f'(x)=\dfrac{g'(x)\,h(x)-g(x)\,h'(x)}{h^2(x)}\) より, \(f'(\alpha)=0\) ならば,
\(g'(\alpha)\,h(\alpha)-g(\alpha)\,h'(\alpha)=0\) すなわち
\(g'(\alpha)\,h(\alpha)=g(\alpha)\,h'(\alpha)\) である。
両辺を \(h(\alpha)\,h'(\alpha)\) で割ると,
\(\dfrac{g'(\alpha)}{h'(\alpha)}=\dfrac{g(\alpha)}{h(\alpha)}\) であるから,
\(f(\alpha)=\dfrac{g(\alpha)}{h(\alpha)}=\dfrac{g'(\alpha)}{h'(\alpha)}\) が成り立つ。(終)
1行目では商の微分の公式を使いました。
定理の意味・使い方
この定理の意味は, 『分数関数の極値を求めるとき, 分母と分子をそれぞれ微分した式におきかえてもよい』ということです。
例えば, 次の分数関数
\(f(x)=\dfrac{2x+1}{x^2+3}\)
が \(x=\alpha\) で極値をもつとすると,
極値は \(f(\alpha)=\dfrac{ 2\alpha +1}{{\alpha}^2+3}=\dfrac{2}{2\alpha}=\dfrac{1}{\alpha}\)
となります。
上式の, 左から2番目の辺から3番目の辺への変形で安田の定理を使いました。
もしも, \(\alpha\) が整数などの簡単な値の場合は, 上式の左から2番目の辺を使っても(つまり安田の定理を使わなくても) \(f(\alpha)\) をすぐに求められます。
一方で, \(\alpha\) が分数や無理数の混じった複雑な値の場合は, 安田の定理を使って最右辺まで変形することで, 計算を楽にできます。
この分数関数の極値を, 次の例題で具体的に求めます。
例題
問題
\(\quad f(x)=\dfrac{2x+1}{x^2+3}\)
解説
\(=\dfrac{(2x+1)'(x^2+3)-(2x+1)(x^2+3)’}{(x^2+3)^2}\,\cdots (*)\)
\(=\dfrac{2(x^2+3)-(2x+1)\cdot 2x}{(x^2+3)^2}\\
=\dfrac{-2x^2-2x+6}{(x^2+3)^2}\\
=\dfrac{-2(x^2+x-3)}{(x^2+3)^2}\)
\(f'(x)=0\) となるのは, \(f'(x)\) の分子が \(0\) になるときです。
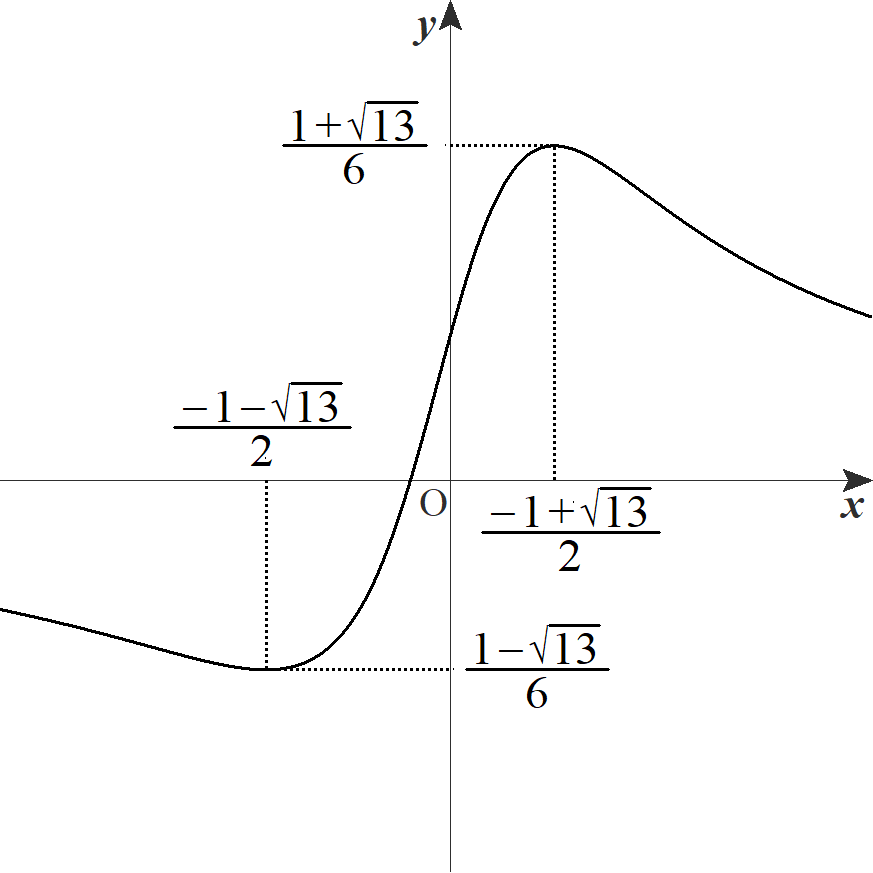
すなわち, \(x^2+x-3=0\) より \(x=\dfrac{-1\pm \sqrt{13}}{2}\) のときです。ここで,
\(\alpha =\dfrac{-1 – \sqrt{13}}{2} \\
\beta =\dfrac{-1\ + \sqrt{13}}{2}\)
とおくと, \(f(x)\) の増減表は次のようになります。
\(\begin{array}{c|ccccc}
x & & \alpha & & \beta & \\
\hline
f'(x) & – & 0 & + & 0 &- \\
\hline
f(x) &\searrow & f(\alpha) & \nearrow & f(\beta) & \searrow\\
\end{array}\)
\(f(x)=\dfrac{2x+1}{x^2+3}\) に \(x=\alpha,\, \beta\) を代入すれば極小値 \(f(\alpha)\) と極大値 \(f(\beta)\) が求まりますが, このまま代入すると計算がやや面倒です。
そこで, 安田の定理を使えば計算を楽にできます。
\(x=\alpha,\,\beta\) のとき, \(f'(x)=0\) より, \((*)\) の分子が \(0\) になるので,
\((2x+1)'(x^2+3)-(2x+1)(x^2+3)’ =0\)
が成り立ちます。よって,
\(f(x)=\dfrac{2x+1}{x^2+3}=\dfrac{(2x+1)’}{(x^2+3)’}=\dfrac{2}{2x}=\dfrac{1}{x}\)
となります。(左から2番目の辺から3番目の辺への変形が安田の定理)
ゆえに,
\(f(\alpha)=\dfrac{1}{\alpha}=\dfrac{2}{-1-\sqrt{13}}=\dfrac{2(-1+\sqrt{13})}{-12}\\
\phantom{f(\alpha)}=\dfrac{1-\sqrt{13}}{6}\)
\(f(\beta)=\dfrac{1}{\beta}=\dfrac{2}{-1+\sqrt{13}}=\dfrac{2(-1-\sqrt{13})}{-12}\\
\phantom{f(\beta)}=\dfrac{1+\sqrt{13}}{6}\)
したがって,
極小値は \(\dfrac{1-\sqrt{13}}{6}\)
極大値は \(\dfrac{1+\sqrt{13}}{6}\)
補足
\(f(x)\) のグラフは次のようになります。
\(\displaystyle\lim_{x \to \pm\infty}f(x)=0\)
