コーシー・シュワルツの不等式:証明
コーシー・シュワルツの不等式を証明します。ベクトルを使う証明方法、判別式を使う証明方法の2通りを紹介します。
例題は別ページで紹介しています。
コーシー・シュワルツの不等式:例題
コーシー・シュワルツの不等式
実数
\(a_1,\,a_2,\cdots ,\,a_n,\,b_1,\,b_2,\cdots ,\,b_n\)
に対して,不等式
\(\color{blue}{({a_1}^2+{a_2}^2+\cdots + {a_n}^2)({b_1}^2+{b_2}^2+\cdots + {b_n}^2)}\)
\(\color{blue}{\quad \geqq (a_1 b_1+a_2 b_2+\cdots + a_nb_n)^2}\)
が成り立つ。
等号は,
\(\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots =\dfrac{a_n}{b_n}\)
のとき成立する。ただし, \(b_i=0\) のときは \(a_i=0\) とする。
ベクトルを使う証明
ベクトルの内積を使います。
\(\vec{b} = (b_1, b_2, \cdots, b_n) \)
\(\vec{a} \) と \(\vec{b}\) のなす角を \(\theta\) とおく。
ベクトルの内積は
\(\vec{a}\cdot \vec{b} =|\vec{a}||\vec{b}|\cos\theta\)
\(-1 \leqq \cos\theta \leqq 1\) より
\(-|\vec{a}||\vec{b}| \leqq \vec{a}\cdot \vec{b} \leqq |\vec{a}||\vec{b}|\)
よって
\(|\vec{a}\cdot\vec{b}| \leqq |\vec{a}||\vec{b}|\quad\) (*補足)
両辺を2乗すると
\((\vec{a}\cdot\vec{b})^2 \leqq |\vec{a}|^2|\vec{b}|^2 \)
ここで,
\((\vec{a}\cdot\vec{b})^2=(a_1 b_1 +a_2 b_2 +\cdots + a_n b_n)^2\)
\(|\vec{a}|^2={a_1}^2+{a_2}^2+\cdots +{a_n}^2\)
\(|\vec{b}|^2={b_1}^2+{b_2}^2+\cdots +{b_n}^2\)
したがって,コーシー・シュワルツの不等式が成り立つ。
等号成立条件の確認
\(\cos\theta=\pm 1\) のとき
\((\vec{a}\cdot\vec{b})^2 = |\vec{a}|^2|\vec{b}|^2 \) となり等号成立。
このとき \(\theta=0^{\circ},180^{\circ}\) であり, \(\vec{a}\) と \(\vec{b}\) は平行。
よって \(\vec{a}=k\vec{b}\) と書ける。
このとき \(a_1= k b_1,\,a_2=kb_2,\cdots\) となり
\(\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots =\dfrac{a_n}{b_n}\,(=k)\) である。
補足
\(-C \leqq x \leqq C \Leftrightarrow |x| \leqq C\)
判別式を使う証明
\((\textbf{実数})^2 \geqq 0\) を使います。
\((a_1-tb_1)^2 +(a_2 -tb_2)^2+\cdots +(a_n -tb_n)^2 \geqq 0\quad \cdots\unicode{x2460}\)
である。\(t\) について降べきの順に整理すると
\(({b_1}^2+{b_2}^2+\cdots + {b_n}^2)t^2-2(a_1 b_1 + a_2 b_2 + \cdots + a_n b_n)t+({a_1}^2 + {a_2}^2 +\cdots + {a_n}^2)\)
\(\geqq 0 \quad\cdots \unicode{x2461}\)
(i) \({b_1}^2+{b_2}^2+\cdots +{b_n}^2\neq 0\) のとき
\(\unicode{x2461}\) の左辺を \(f(t)\) とおき, \(f(t)\) の判別式を\(D\) とおくと,
\(D/4\)
\(=(a_1b_1+a_2b_2+\cdots +a_n b_n)^2 -({a_1}^2 + {a_2}^2 +\cdots + {a_n}^2)({b_1}^2+{b_2}^2+\cdots + {b_n}^2)\)
\(\leqq 0 \quad\cdots\unicode{x2462}\) (補足)
よって,コーシー・シュワルツの不等式が成り立つ。
(ii) \({b_1}^2+{b_2}^2+\cdots +{b_n}^2=0\) のとき
\(b_1=b_2=\cdots=b_n=0\) だから \(\unicode{x2462}\)が成り立つ。
等号成立条件の確認
\(a_1 -tb_1=0,\,a_2-tb_2=0,\,\cdots ,\,a_n-tb_n=0\) のとき \(\unicode{x2460}\) の等号が成立する。
このとき
\(\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots =\dfrac{a_n}{b_n}\,(=t)\) である。
補足
係数が長くて分かりにくいですが, \(f(t)\) は \(t\) の2次式です。
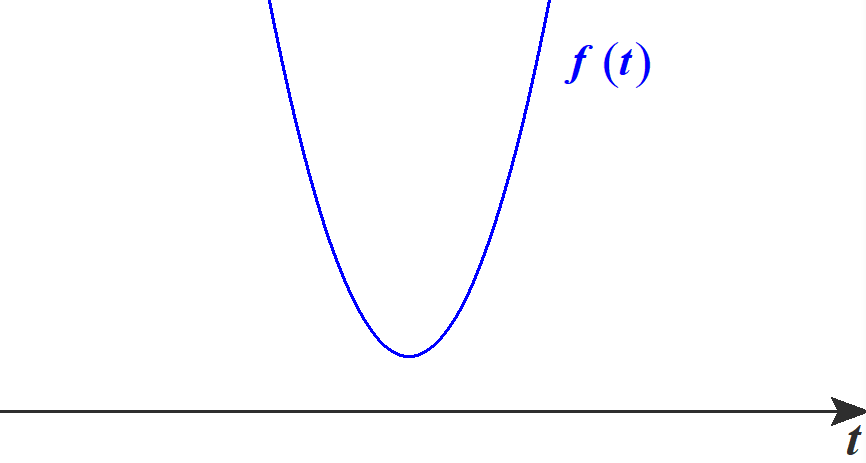
\(t^2\) の係数が正なので, \(f(t)\) は下に凸です。
任意の実数 \(t\) で \(f(t)\geqq 0\) が成り立つとき, 判別式は\(D\leqq 0\) です。
