正多角形の場合の数
正多角形の対角線の数、正多角形の頂点で作る三角形についての場合の数を考えます。
正八角形ぐらいまでなら手書きで考えられるかもしれませんが、それ以上になると手書きでは難しいと思います。
一般化して正n角形で考えてみることで、どの正多角形についても答えられるようになるでしょう。
対角線の個数
問題
解答
このうち \(n\) 本は対角線ではなく辺である。(隣り合う2点を選んだとき辺になる)
よって, 対角線の本数は
\({}_n{\rm{C}}_2 -n\) 本
例
三角形の対角線: \({}_3{\rm{C}}_2-3=0\) 本
四角形の対角線: \({}_4{\rm{C}}_2-4=2\) 本
辺を共有する三角形の個数
問題
(1) 三角形は何個あるか。
(2) 正\(n\)角形と1辺のみを共有する三角形は何個あるか。
(3) 正\(n\)角形と辺を共有しない三角形は何個あるか。
\(n\) は \(4\) 以上の整数とする。
解答
\({}_n{\rm{C}}_3=\color{red}{\dfrac{n(n-1)(n-2)}{6}}\) 個
(2)
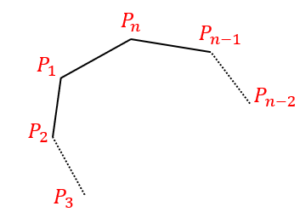
正\(n\)角形の頂点を \(P_1,P_2,\cdots,P_n\) とおく。
1辺を共有するとき,その辺の選び方は \(n\) 通りある。
(\(P_1P_2,\,P_2P_3,\,\cdots,\,P_nP_1)\)
\(P_nP_1\) を共有する1辺として選んだとき,
残りの1点は \(P_1,\,P_2,\,P_{n-1},\,P_n\) 以外の
\(n-4\) 個から選ぶ。
(\(P_2\) や \(P_{n-1}\) を選ぶと2辺を共有してしまうため)
他の辺を選んだ時も同様。
よって求める三角形の個数は
\(\color{red}{n(n-4)}\) 個
例
正六角形: 12個
正八角形: 32個
(3)
2辺を共有する三角形の個数は \(n\) 個
(\(\triangle P_1P_2P_3,\,\triangle P_2P_3P_4,\,\cdots,\,\triangle P_nP_1P_2\))
3辺を共有する三角形は無い
(3辺を共有する場合, 頂点の数は少なくとも4個あり三角形にはならない)
よって, 辺を共有しない三角形の個数は
\(\color{red}{\dfrac{n(n-1)(n-2)}{6}\,-\,n(n-4)\,-\,n}\) 個
(三角形の総数から, 1辺を共有する三角形と2辺を共有する三角形を除いた)
例
正六角形: 2個
正八角形: 16個
直角三角形の個数
問題
正多角形の頂点は外接円の周上にあります。
直径に対する円周角は直角であることを使います。
解答
それぞれの直径について残りの1点の選び方は \(2n-2\) 通りある。
よって, 直角三角形の数は
\(n\cdot(2n-2)\)
\(=\color{red}{2n(n-1)}\) 個
例
正六角形:
\(2n=6\) のとき \(n=3\)
よって, 直角三角形の数は
\(2\cdot 3\cdot(3-1)=12\) 個
正八角形:
\(2n=8\) のとき \(n=4\)
よって, 直角三角形の数は
\(2\cdot 4\cdot(4-1)=24\) 個
